삼분 탐색(Ternary Search)

삼분 탐색

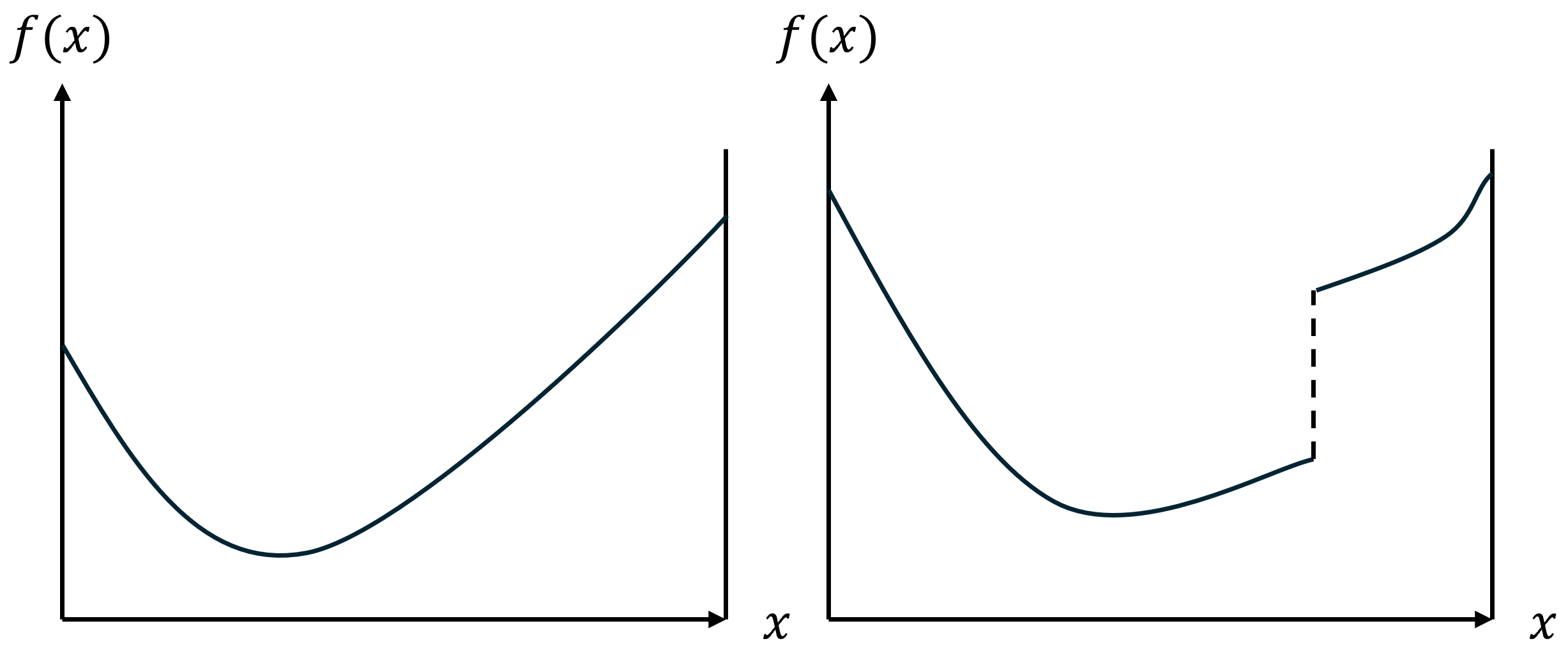
어떤 unimodal한 그래프에서, 최대/최소 값을 O(logN)에 찾는 알고리즘

 

unimodal은 단조 증가와 단조 감소로 이분되는 그래프로 아래 그림과 같다.

이런 값들의 나열에 대해서 삼분 탐색을 가능하고, 만약 같은 값이 연속되는 평평한 구간이 존재하는 경우 사용 불가능하다.

unimodal graphs

 

 

 

삼분 탐색 알고리즘 과정

1. unimodal한 구간에 대해 삼분 탐색을 수행

2. 구간을 3개로 나누어서 탐색, [O, A], [A, B], [B, N]

3. f(A)가 f(B)보다 크다면, [O, A]에는 최솟값이 존재할 수 없으므로, 구간을 [A, N]으로 축소

4. 2 ~ 3 과정을 반복

5. 남은 구간3개의 후보 값에 대해 완전 탐색

 

이분 탐색과 과정은 비슷한데, 3개의 구간에 대해 탐색 영역을 줄여나가면서 진행하고 최종적으로 구간이 남기 때문에 구간에 대한 완탐을 해서 최소값을 찾아준다.

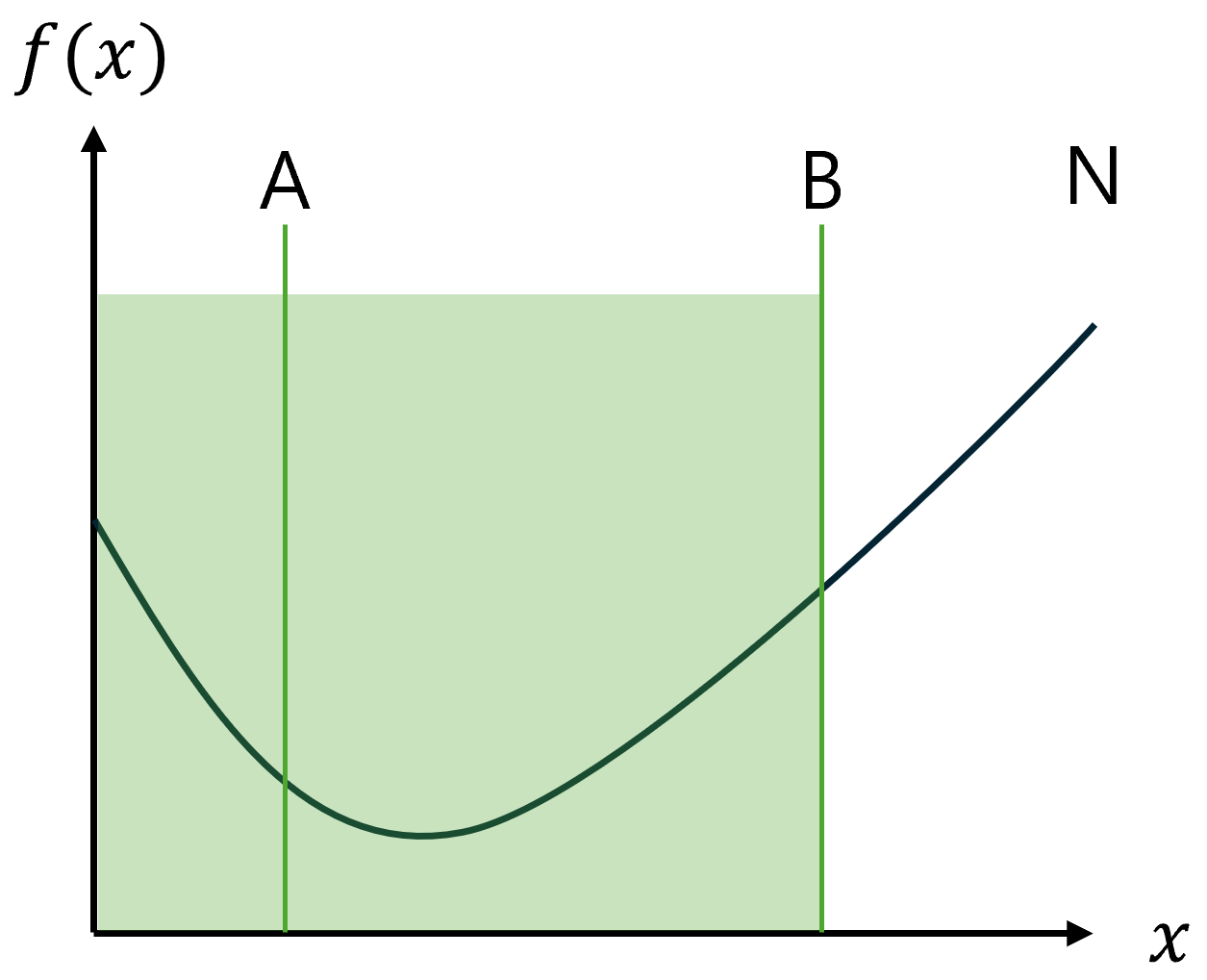
f(A) < f(B) 이므로 최솟값은 [O, B]에 존재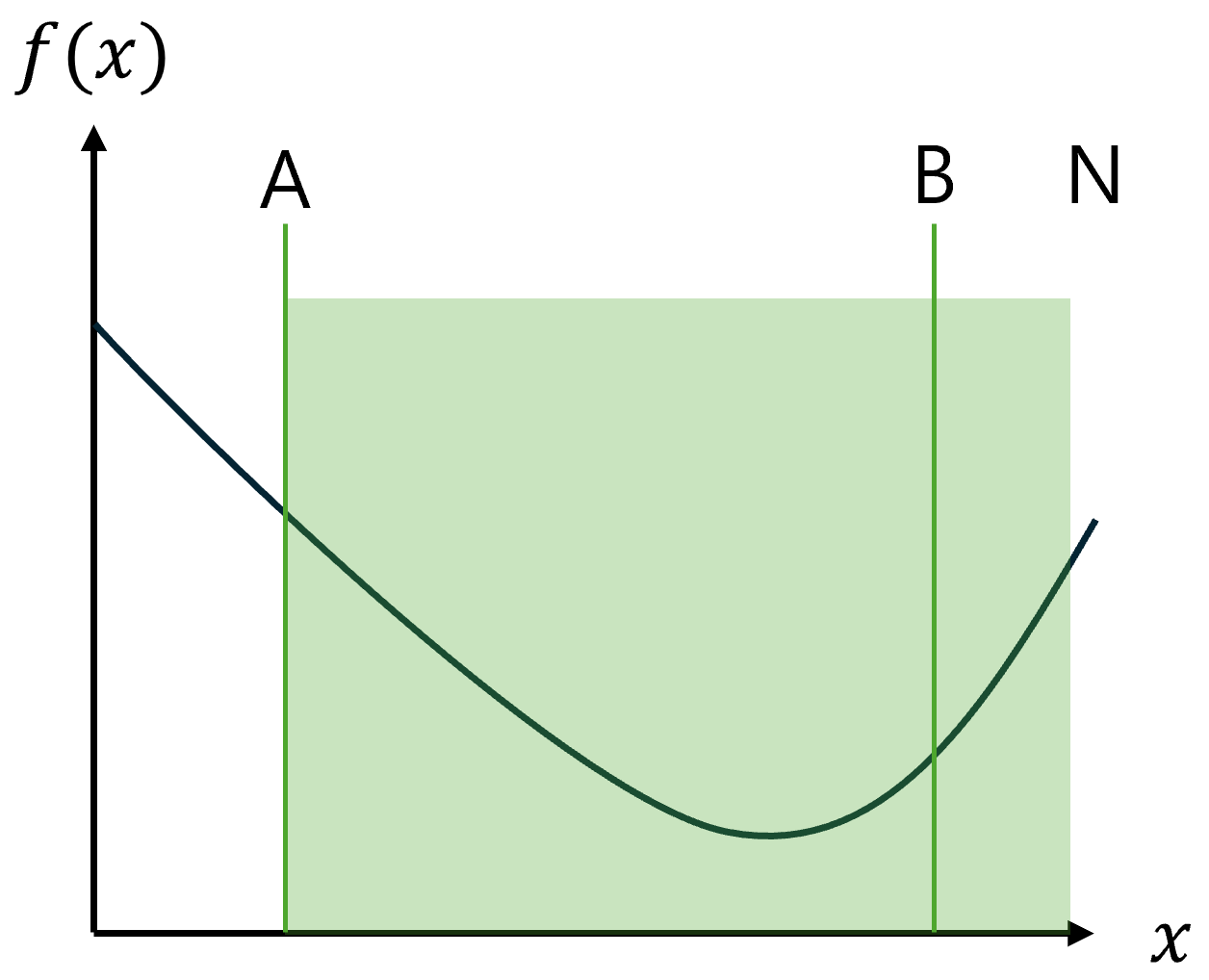

f(A) > f(B) 이므로 최솟값은 [A. N]에 존재

 

 

 

예시 코드

문제(https://www.acmicpc.net/problem/8986)에 대한 삼분 탐색 풀이

삼분 탐색은 풀이 자체는 간단한데, 삼분 탐색인지 구분하는게 쉽지 않은 것 같다.

#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <map>
#include <cmath>
using namespace std;
int N;
int arr[100000];
long long check(int n) {
	long long sum = 0;
	for (int i = 1; i < N; ++i) {
		sum += abs((long long)n * i - arr[i]);
	}
	return sum;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin >> N;
	for (int i = 0; i < N; ++i) {
		cin >> arr[i];
	}
	long long left = 0;
	long long right = 1000000000;
	while (right - left >= 3) {
		long long lm = (left * 2 + right) / 3;
		long long rm = (right * 2 + left) / 3;
		if (check(lm) < check(rm)) {
			right = rm;
		}
		else {
			left = lm;
		}
	}
	long long ans = 100000000000000;
	for (int i = 0; i < 3; ++i) {
		ans = min(ans, check(left + i));
	}
	cout << ans;
	return 0;
}