-
회전하는 캘리퍼스(Rotating Calipers)알고리즘/Algorithm Theory 2025. 1. 29. 04:09
개요
한동안 바빠서 새 알고리즘을 공부할 틈이 없었는데, 연휴 기념 오랫만에 들고온 기하 알고리즘 ~
아래 내용은 CCW와 Convex Hull에 대한 이해를 바탕으로 한다.
CCW: https://doraeul19.tistory.com/297
Convex Hull: https://doraeul19.tistory.com/343
회전하는 캘리퍼스(Rotating Calipers)
캘리퍼스는 아래와 같이 길이를 측정하는 도구로, 회전하는 캘리퍼스 알고리즘은 볼록 다각형을 돌면서 두 지점간의 거리를 구하는 알고리즘이다.

캘리퍼스 지지선과 대척점
지지선(A line of support): 볼록 다각형에 대해 점이나 변에 접한 직선

지지선 대척점(Anti podal points): 평행한 두 지지선이 있을 때, 그 지지선에 닿아있는 두 점(A와 B는 대척점, A와 C는 대척점)
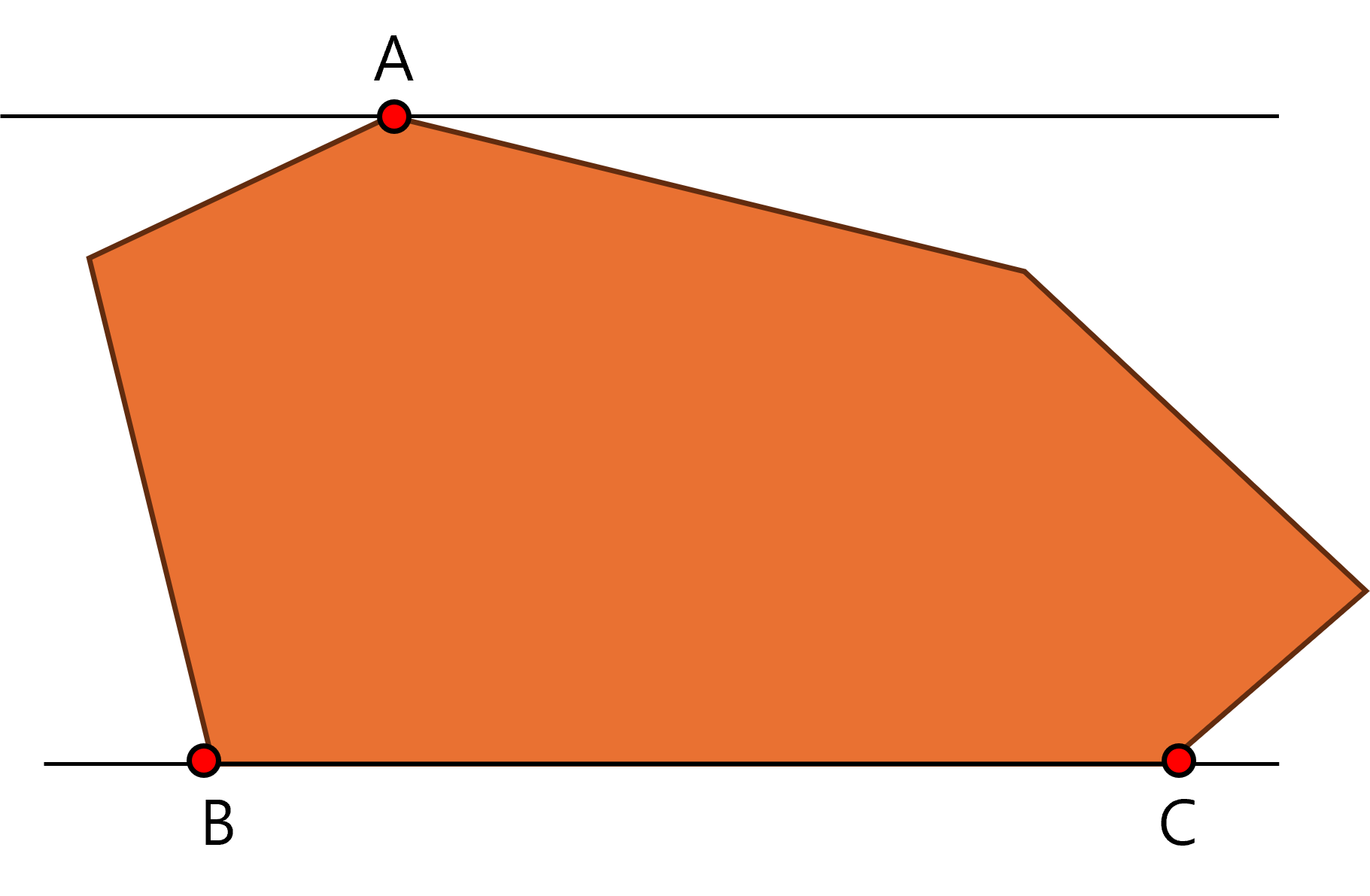
대척점 회전하는 캘리퍼스 과정
직경: 평행한 두 지지선의 거리 중 가장 큰 것 → 대척점 중 거리가 가장 긴 것 → 지지선 두 개로 볼록 다각형을 돌면서 거리 구하기
1. Convex Hull 구하기
2. 두 개의 지지선에 대해 거리 구하기
3. 두 개의 지지선에 대해 CCW 구하기
4. CCW가 음수/양수(시계/반시계)일 경우 인덱스 증가
5. 한 바퀴 돌 때 까지 2~4번을 반복
이게 뭔 소리인가? 하겠지만 그림으로 보면 쉽게 이해가능하다.
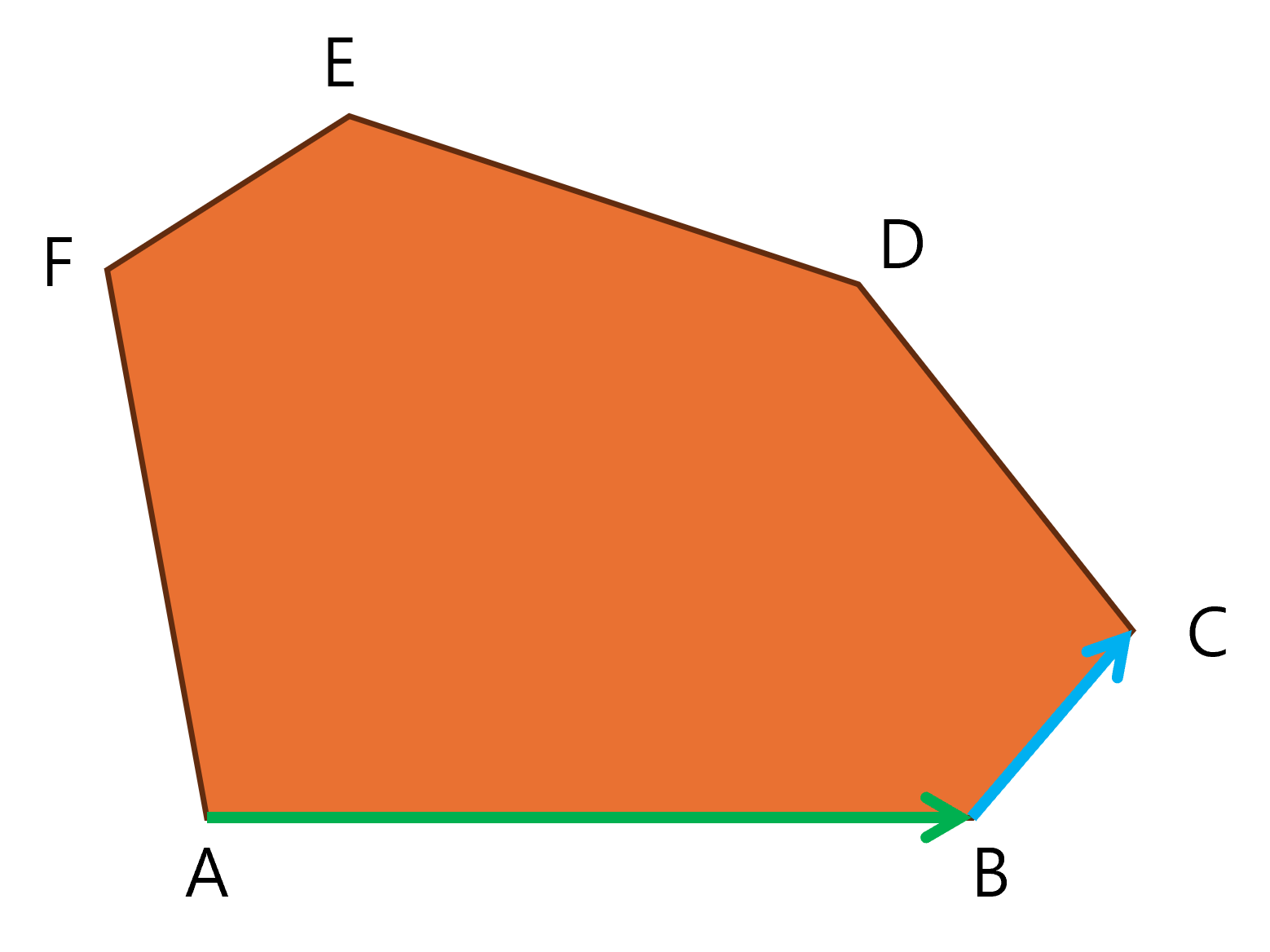
일단 각각 AB, BC로 시작한다고 하고, 각각 지지선1, 지지선2라고 하자 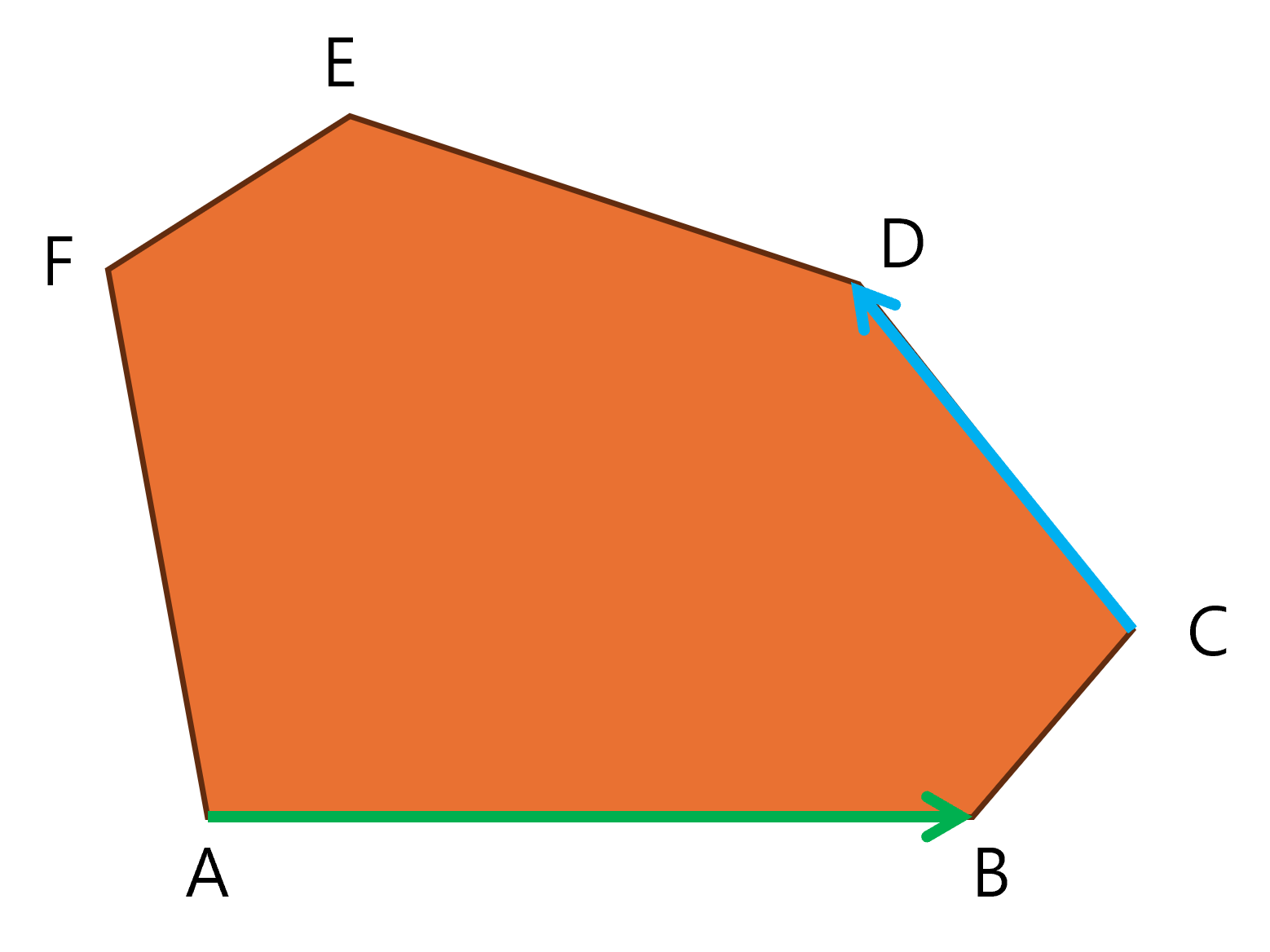
AB와 BC의 CCW가 양수이므로 지지선2를 한 칸 민다. 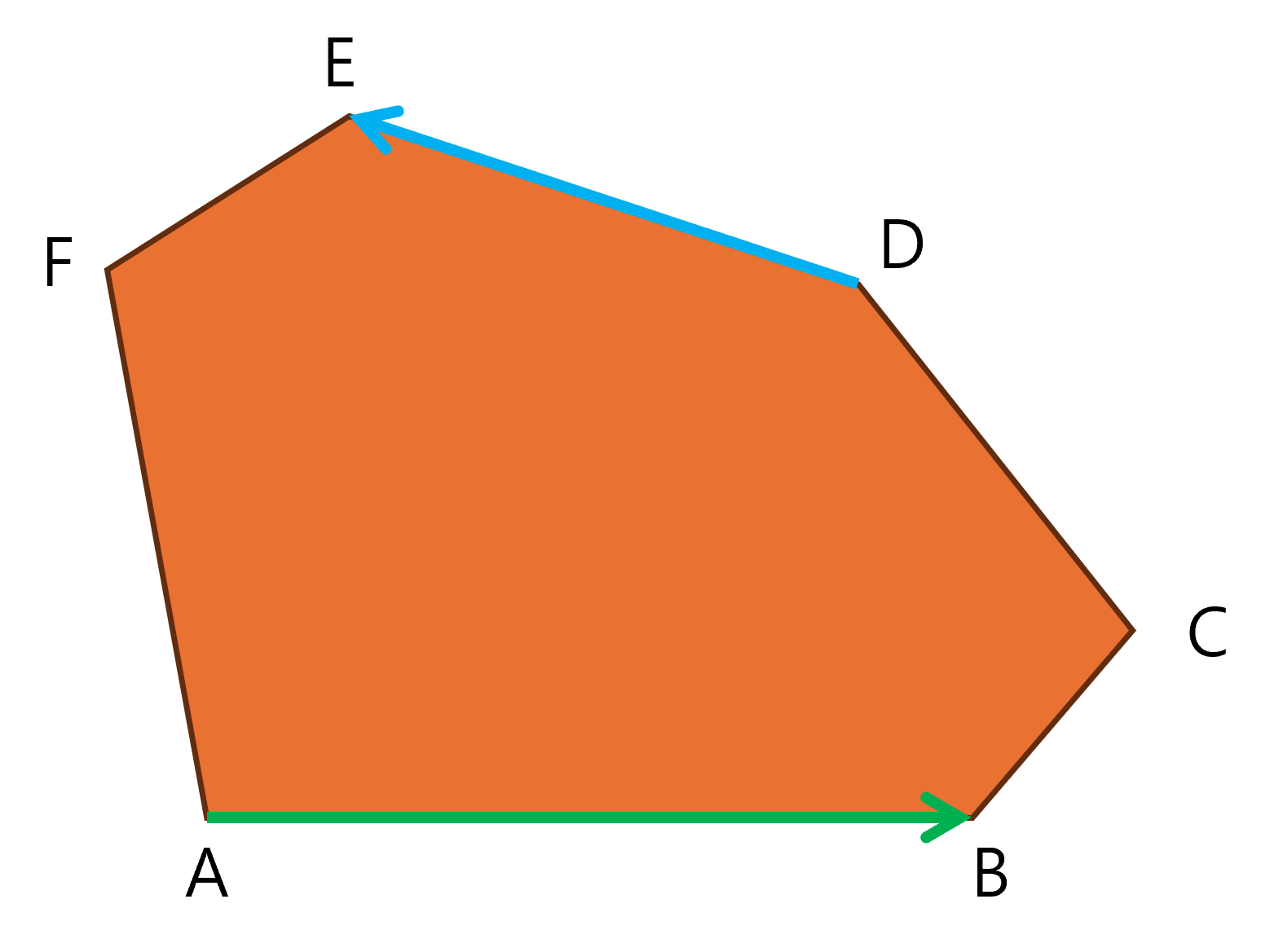
마찬가지로 AB와 CD의 CCW가 양수이므로 지지선2를 한 칸 민다. 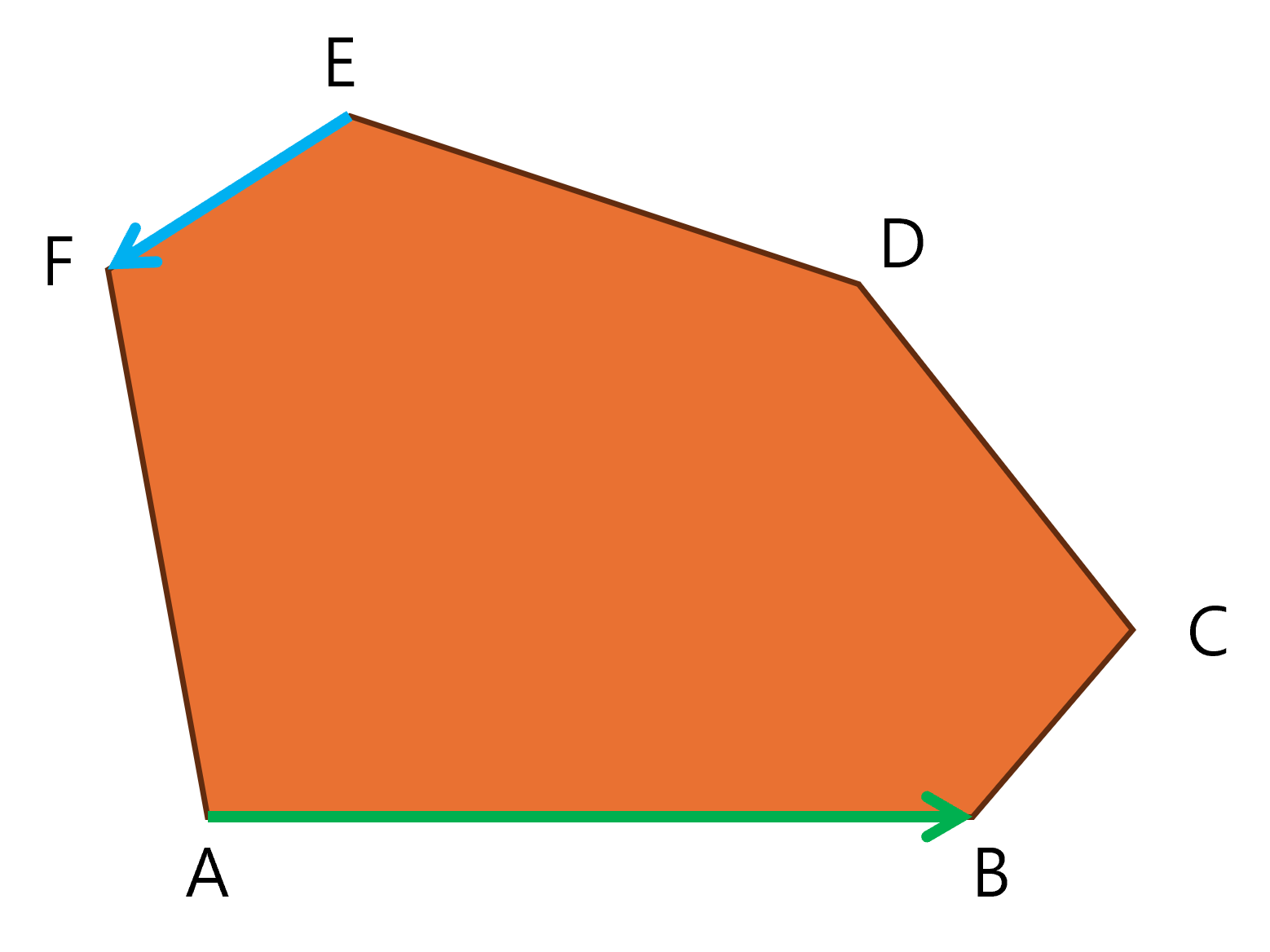
마찬가지 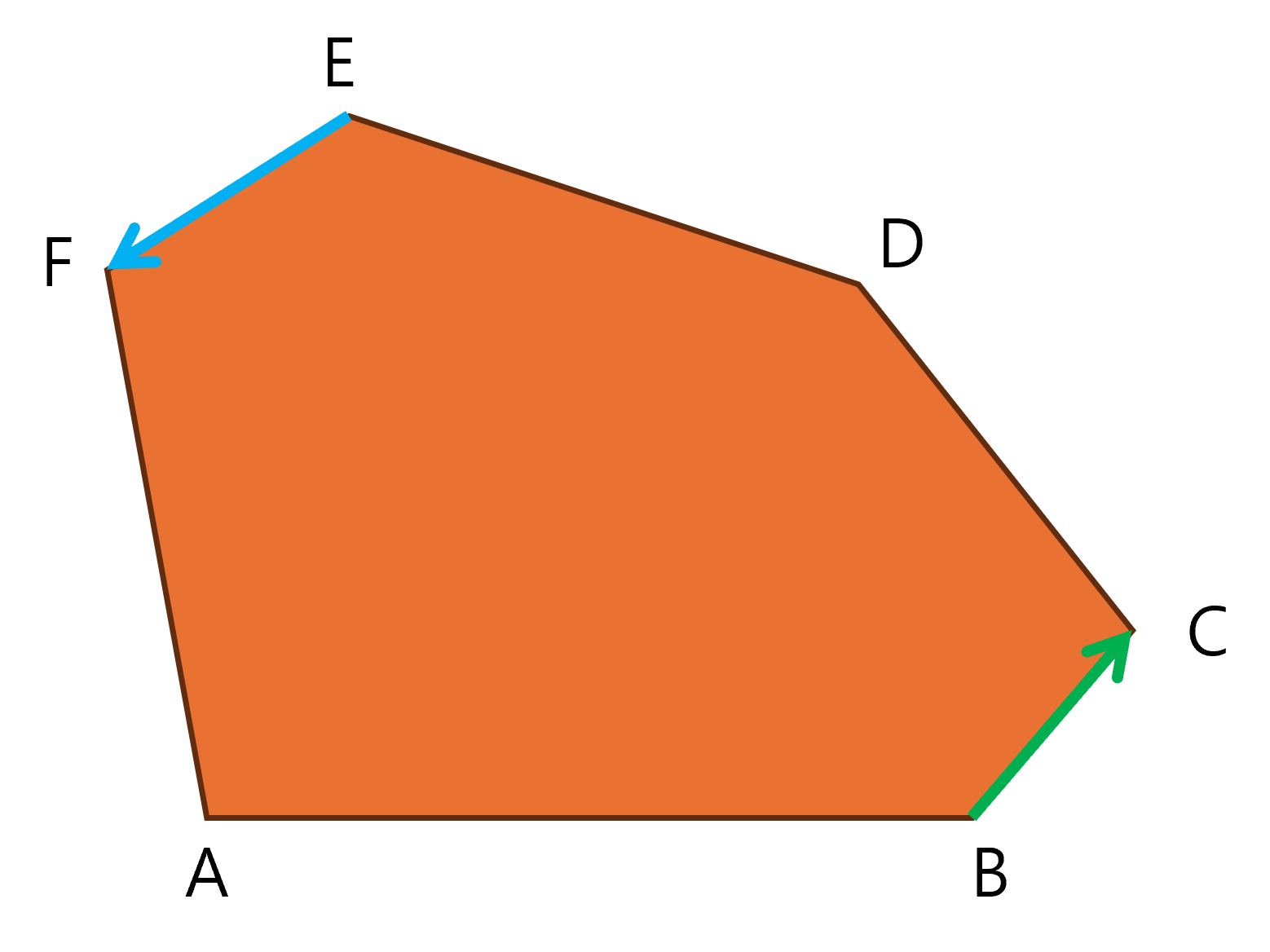
드디어 CCW < 0 이므로 이제 지지선1을 한 칸 민다. 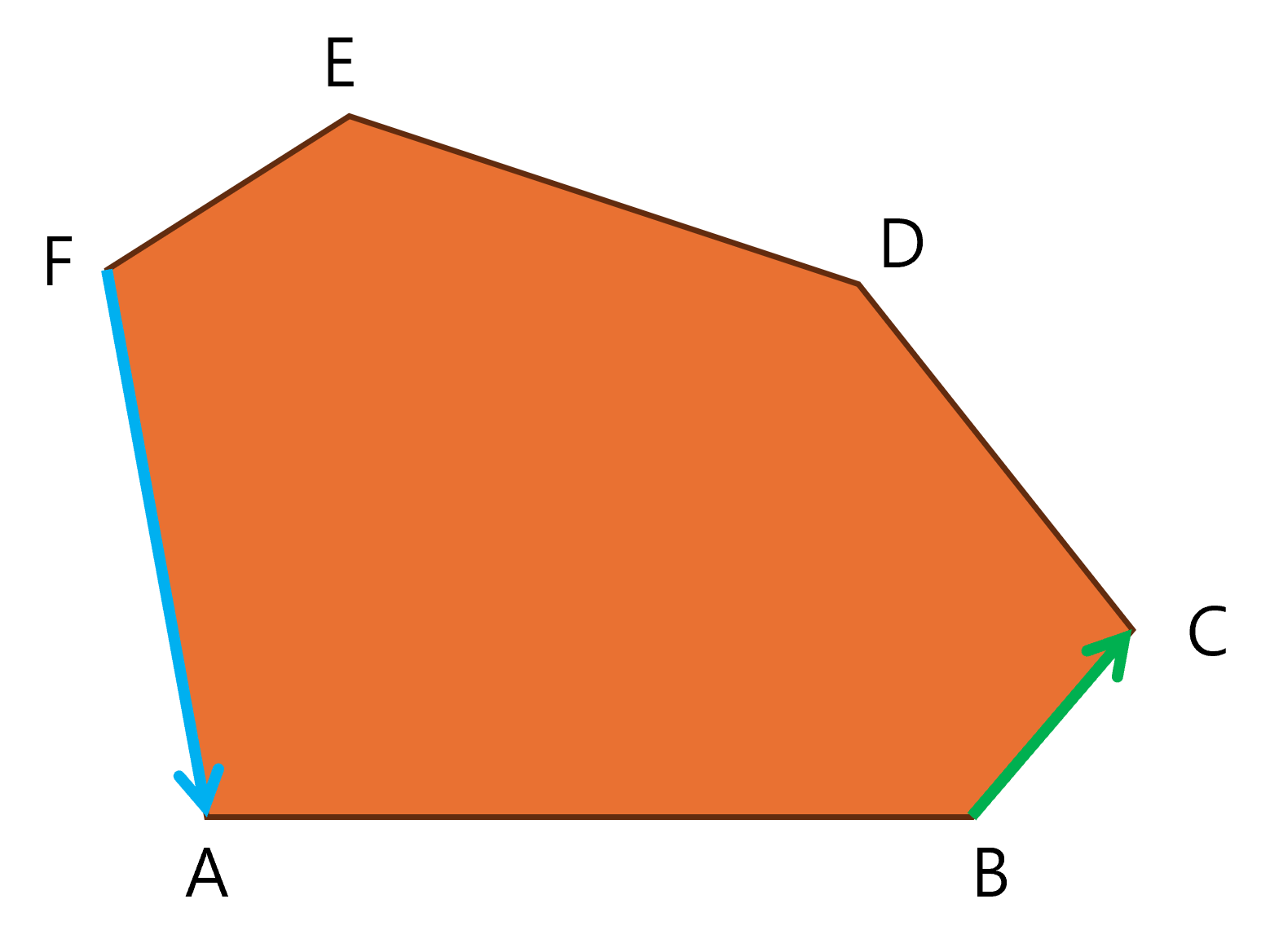
다시 CCW > 0 이므로 지지선2를 한 칸 민다. 이하 생략 ...
위와 같은 과정을 계속 반복하면서 한 바퀴를 돌면 된다.
직관적으로 보면 두 직선이 이루는 각에 따라 두 직선 사이의 거리가 증가할지 감소할지 결정되기 되기 때문에 투 포인터처럼 돌려주면 된다.
예시 코드
문제(https://www.acmicpc.net/problem/2049)에 대한 코드 볼록 다각형을 만들고 캘리퍼스를 돌리면 되는 문제이다.
스택을 벡터로 변환하다 보니 시계 방향으로 캘리퍼스를 회전시켰다.
#include <iostream> #include <vector> #include <queue> #include <stack> #include <algorithm> #include <map> #include <cmath> using namespace std; struct Dot { int x, y; }; int N; vector<Dot> input; stack<Dot> s; vector<Dot> convexHull; int cross(Dot& a, Dot& b, Dot& c) { Dot line1 = { b.x - a.x, b.y - a.y }; Dot line2 = { c.x - b.x, c.y - b.y }; int r = line1.x * line2.y - line1.y * line2.x; if (r < 0) return -1; if (r > 0) return 1; return 0; } int cross2(Dot& a, Dot& b, Dot& c, Dot& d) { Dot line1 = { b.x - a.x, b.y - a.y }; Dot line2 = { d.x - c.x, d.y - c.y }; int r = line1.x * line2.y - line1.y * line2.x; if (r < 0) return -1; if (r > 0) return 1; return 0; } int getDistance(Dot a) { //Dot0과의 distance return (input[0].x - a.x) * (input[0].x - a.x) + (input[0].y - a.y) * (input[0].y - a.y); } bool cmp(Dot& a, Dot& b) { int r = cross(input[0], a, b); if (r > 0) return 1; if (r == 0) return getDistance(a) < getDistance(b); return 0; } int main() { ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); cin >> N; int aaa, bbb, taa, tbb; cin >> aaa >> bbb; input.push_back({ aaa , bbb }); for (int i = 1; i < N; ++i) { cin >> aaa >> bbb; if (aaa < input[0].x) { taa = input[0].x; tbb = input[0].y; input[0] = { aaa, bbb }; input.push_back({ taa, tbb }); } else if (aaa == input[0].x && bbb < input[0].y) { taa = input[0].x; tbb = input[0].y; input[0] = { aaa, bbb }; input.push_back({ taa, tbb }); } else { input.push_back({ aaa, bbb }); } } sort(input.begin() + 1, input.end(), cmp); s.push(input[0]); s.push(input[1]); for (int i = 2; i < input.size(); ++i) { while (s.size() >= 2) { Dot prev = s.top(); s.pop(); Dot prev2 = s.top(); if (cross(prev2, prev, input[i]) > 0) { s.push(prev); break; } } s.push(input[i]); } while (!s.empty()) { convexHull.push_back(s.top()); s.pop(); } int index = 1; int maxDis = 0; int cs = convexHull.size(); for (int i = 0; i < cs; ++i) { while (cross2(convexHull[i], convexHull[(i + 1) % cs], convexHull[index % cs], convexHull[(index + 1) % cs]) < 0) { //cout << "(" << convexHull[i].x << ", " << convexHull[i].y << ")" << // " "<< "(" << convexHull[index % cs].x << ", " << convexHull[index % cs].y << ")" << "\n"; int currDis = (convexHull[i].x - convexHull[index % cs].x) * (convexHull[i].x - convexHull[index % cs].x) + (convexHull[i].y - convexHull[index % cs].y) * (convexHull[i].y - convexHull[index % cs].y); if (maxDis < currDis) { maxDis = currDis; } index++; } //cout << "(" << convexHull[i].x << ", " << convexHull[i].y << ")" << // " " << "(" << convexHull[index % cs].x << ", " << convexHull[index % cs].y << ")" << "\n"; int currDis = (convexHull[i].x - convexHull[index % cs].x) * (convexHull[i].x - convexHull[index % cs].x) + (convexHull[i].y - convexHull[index % cs].y) * (convexHull[i].y - convexHull[index % cs].y); if (maxDis < currDis) { maxDis = currDis; } } cout << maxDis; return 0; }'알고리즘 > Algorithm Theory' 카테고리의 다른 글
삼분 탐색(Ternary Search) (0) 2025.01.30 Trie 트라이 (4) 2024.12.21 체비쇼프 거리 (3) 2024.03.24 라빈-카프, 접미사 배열, lcp 배열 (1) 2024.03.24 세그먼트 트리 (Segment Tree) (1) 2024.03.12