체비쇼프 거리

체비쇼프 거리 Chebyshev Distance

 

유클리드 거리와, 맨허튼 거리 외에도 체비쇼프 거리라는 것이 있다.

솔직히 특별한 거리는 아니고, 맨허튼 거리가 8 방향에 대해 적용되는 것이라고 보면된다.

 

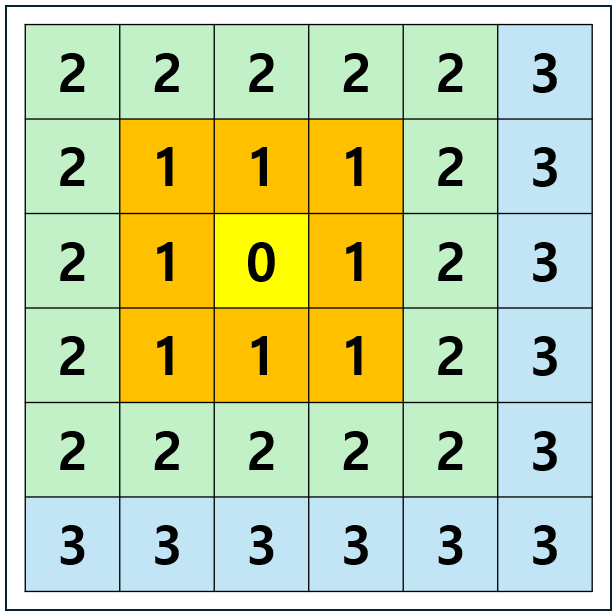
격자에서의 각 거리

 

노랑색 칸 부터 다른 칸들에 대해 체비쇼프 거리를 나타내면 다음과 같다. 

Flood Fill(BFS) 를 8 방향으로 돌려 얻거나, 격자의 좌표의 차이의 최대 값이 거리가 된다.

strcut yx{ int y, x };
yx a, b;
int distance = max(abs(a.x - b.x), abs(a.y - b.y));

 

 

 

 

 

https://www.acmicpc.net/problem/28452(체비쇼프 거리를 활용한 시뮬레이션 문제)

28452번: 탄막 게임

탄막은 항상 플레이어를 향해 이동하기 때문에, 플레이어는 탄막을 피할 수 없고,

탄막이 도달하는데 가장 시간이 오래걸리는 곳으로 도망가는 것이 가장 오래 살아남을 수 있는 방법이 된다.

 

탄막과 플레이어 각각 (y, x) 좌표에 도달할 수 있는 체비쇼프 거리를 모두 구해서 T 초 동안 살아남을 수 있는지 체크하면 해를 구할 수 있다.