-
[Divide-and-Conquer] 분할정복알고리즘/Algorithm Theory 2022. 6. 20. 22:49
분할 정복 : 말그대로 문제를 분할하여 정복하여 풀이
- 분할 정복의 대표적인 예시 : Merge Sort
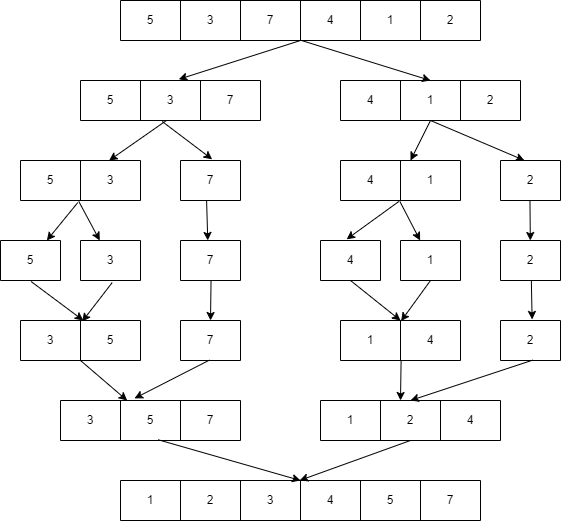
병합정렬
1. 주어진 배열을 두 부분으로 나눈다.
2. 두 부분배열을 각각 Mergesort한다.
3. 정렬된 부분배열을 합쳐서(merge) 하나의 정렬된 배열로 만든다.
MergeSort(A[1...n]): if n > 1: m = [n/2] MergeSort(A[1...m]) MergeSort(A[m+1...n]) Merge(A[1...n], m)
- Divide and Conqur의 설계
1. 문제를 동일한 작은 문제들로 나누어라
2. 각각의 작은 문제들을 재귀요정에게 맡겨라(일단 같은 작은 문제들을 던져주면 알아서 해결해준다.)
3. 최종 해결법은 작은 문제들에 대한 답을 결합해라.
* 어떤 작은 문제들이 특정한 사이즈 아래로 떨어지면, 재귀없이 직접 또는 무차별대입으로 풀수있다.
(위의 mergesort에서는 n이 1이되는 순간이 임계점이 된다.)
ex1)
SUM(1...n) 에 대해 recursion으로 구현해보자 : 1부터 n까지의 합
위 문제에 대해 점화식을 생각해 볼 수 있다.
f(n)은 n까지의 합이라고 했을 때, 점화식은 아래와 같다.
f(n) = 1 (n=1일 때)
f(n) = f(n-1) + n (n>1일 때)점점 n보다 작은 사이즈로 문제의 크기를 줄여나가고, 문제의 크기가 n=1이 됬을 때는 1이라는 답을 낼 수 있다.
즉, 재귀를 사용해 일단 문제의 크기를 줄여나가면, 어느순간 전체문제가 풀리게된다.
- Recursion Tree
말그대로 재귀를 트리로 보이는 것이다.
점화식 : T(n) = 2T(n/2) + O(n)
// 문제의 크기를 반으로 줄인것을 두번 반복하고, 병합하는 과정은 복잡도 n만큼을 가지기 때문에 위와 같은 점화식을 가진다.

mergesort의 recursion tree 위는 합병정렬의 재귀트리의 일부이다.
각 n , n/2, n/4는 문제의 size이다. 즉 한번의 분할을 하면 n에서 n/2로 문제의 size가 줄어든다.
위 과정을 문제의 size가 1이 될때 까지 반복한다.
트리를 통해 알고리즘의 복잡도 또한 구해볼수있다. 트리의 높이를 h라 할때 다음과 같이 계산 가능하다.

에서 (1/2)의 h승을 넘기고, 양변에 로그를 취하면,

그리고 트리의 너비는 n/2+n/2 = n
n/4 + n/4 + n/4 + n/4 = n
n/8 + ... + n/8 = n
즉 트리의 각 층에서 너비는 n이다.
따라서 트리의 size는 너비*높이 , nlogn이 되고, 합병정렬의 복잡도는 O(nlogn) 이다.
'알고리즘 > Algorithm Theory' 카테고리의 다른 글
[Backtracking] Subset Sum (0) 2022.06.25 [D&C] Binary Search (0) 2022.06.25 [Master Theorem] 마스터 이론(정리) (0) 2022.06.20 [Recursion] 재귀 with Hanoi Tower (0) 2022.06.17 [Time Complexity] 시간 복잡도 (0) 2022.06.17