[Recursion] 재귀 with Hanoi Tower

재귀.!, 알고리즘의 이해와 설계에 매우 중요한 기술

 

Recursion의 예.

 

1. 팩토리얼 연산

 

 

 

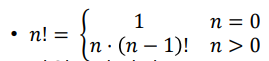
2. 자연수의 정의

  - 1은 자연수이다. (Base case)

  - n이 자연수이면, n보다 1큰수도 자연수이다.

 

---

 

Reduction (= 축소)

어떤 문제X에 대해 Y로 축소해라.

X라는 문제를 풀기위해, Y를 푸는 함수를 호출한다. 이때 Y를 어떻게 풀것인지는 신경쓰지않는다.

이때, Y를 푸는 함수는 어떻게 작동하는지는 모르지만(신경x), 항상 옳게 Y를 풀어낸다.

 

 

Example

- 배열 A[0...n-1]에서 최소값 찾기

1. A를 정렬한다.

2. return A[0]

- Selction(A[0...n-1], k)  배열 A[0...n-1]에서 k번째로 작은 값 찾기

1. A를 정렬한다.

2. return A[k-1]

 

정렬을 어떻게 하든 상관은 없지만, 정렬을 하면 Selection이 풀림, 즉 정렬에 대해서는 신경x

>> Selection을 풀기위해, 정렬문제로 reduce하여 해결

 

---

다시 Recursion으로 돌아와보자.

Recursion은 같은 문제로의 Reduction이다.

재귀에서 Reduction이 어떻게 적용되는지, 다음 하노이타워문제를 예시로 볼 수 있다.

 

Hanoi Tower Algorithm

n개의 원판과 3개의 기둥으로 이루어져있다.

n개의 원판을 다른 기둥으로 옮기는 최소의 move횟수는??

* 단, 큰 원판이 보다 작은 원판 위에 올라갈수없다.

 

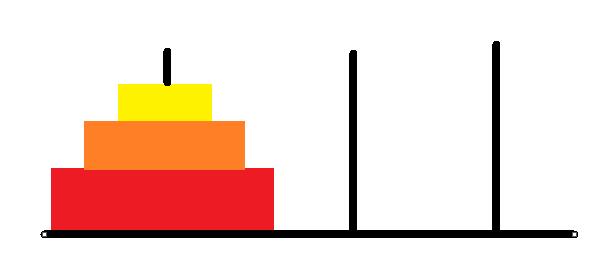
- 3개의 원판을 맨 오른쪽 기둥으로 옮기기는 아래와 같은 방법으로 옮길수있다.

1. 2개의 원판을 가운데 기둥으로 옮긴다.

2. 가장 큰원판을 오른쪽 기둥으로 옮긴다.

3. 2개의 원판을 오른쪽 기둥으로 옮긴다.

이때, 2개의 원판을 어떻게 옮길지는 생각하지 않아도 된다.

 

좀더 일반화해보면,

n개의 원판을 맨 오른쪽 기둥으로 옮기는 것은

1. n-1개의 원판을 가운데 기둥으로 옮긴다.

2. 가장 큰원판을 오른쪽 기둥으로 옮긴다.

3. n-1개의 원판을 오른쪽 기둥으로 옮긴다.

 

* X라는 문제를 풀기위해, Y를 푸는 함수를 호출한다. 이때 Y를 어떻게 풀것인지는 신경쓰지않는다.

이때, Y를 푸는 함수는 어떻게 작동하는지는 모르지만(신경x), 항상 옳게 Y를 풀어낸다.

X : n개의 원판을 맨 오른쪽 기둥으로 옮기는 것

Y : n-1개의 원파을 옮기는 것

즉, 우리는 n-1개를 어떻게 옮기는지에 대해서는 신경쓰지않아도, 항상 옳게 n-1개는 옮겨진다.

 

즉 아래와 같이 재귀를 이용해 Hanoi Tower 알고리즘을 기술할 수 있다.

HANOI(n, src, dst, tmp):
	if n > 0:
    	HONOI(n-1, src, tmp, dst)	//recursion
        move n to from src to dst	// 가장 큰 디스크를 dst로 이동
        HONOI(n-1, tmp, dst, src)	//recursion