Vector Class

https://github.com/oreillymedia/physics_for_game_developers_2e

GitHub - oreillymedia/physics_for_game_developers_2e

---

 

1. Vector Class Methods

 

1.1 크기 (Magnitude)

벡터의 크기

 

inline float Vector::Magnitude(void)
{
	return (float) sqrt(x*x + y*y + z*z);
}

 

 

 

1.2 정규화 (Normalize)

- 벡터를 단위벡터로 정규화

정규화 된 벡터의 길이는 1 임

 

 

벡터 v가 v(x, y, z)의 성분을 가진다면, 각 단위 벡터는 v의 크기로 각각의 성분을 나누면 얻을 수 있다.

//tol은 float 자료형의 오차허용치
float const tol = 0.0001f;

inline void Vector::Normalize(void)
{
    float m = (float)sqrt(x * x + y * y + z * z);
    if (m <= tol) m = 1;
    x /= m;
    y /= m;
    z /= m;

// float 형의 abs 
    if (fabs(x) < tol) x = 0.0f;
    if (fabs(y) < tol) y = 0.0f;
    if (fabs(z) < tol) z = 0.0f;
}

 

 

 

1.3 역 (Reverse)

- 말 그대로 역, 벡터의 방향을 뒤집음, 각 성분의 부호를 뒤집는다.

inline void  Vector::Reverse(void)
{
    x = -x;
    y = -y;
    z = -z;
}

 

 

 

1.4 벡터 합 (operator+=(Vector u))

1.5 벡터 뺄셈 (operator-=(Vector u))

-  마찬가지로 각각의 성분별로 연산한다.

- 벡터의 뺄셈은 두 번째 벡터의 역을 더한 것과 동일하다.

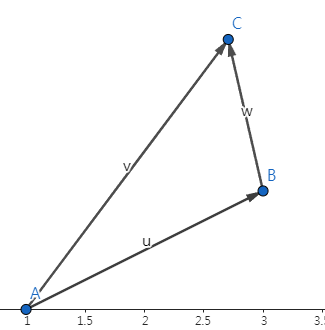
u + w = v

inline Vector & Vector::operator+=(Vector u)
{
    x += u.x;
    y += u.y;
    z += u.z;
    return *this;
}

inline Vector & Vector::operator-=(Vector u)
{
    x -= u.x;
    y -= u.y;
    z -= u.z;
    return *this;
}

 

 

 

1.6 스칼라 곱 (operator*=(float s))

1.7 스칼라 나눗셈 (operator/=(float s))

inline Vector & Vector::operator*=(float s)
{
    x *= s;
    y *= s;
    z *= s;
    return *this;
}

inline Vector & Vector::operator/=(float s)
{
    x /= s;
    y /= s;
    z /= s;
    return *this;
}

 

 

 

1.8 역벡터 (operator-(void))

- 앞선 Reverse와 동일하지만, 새 벡터를 반환한다.

inline Vector Vector::operator-(void)
{
    return Vector(-x, -y, -z);
}

 

 

 

2. Vector Funtions and Operator

2.1 벡터 합

2.2 벡터 뺄셈

inline Vector operator+(Vector u, Vector v)
{
    return Vector(u.x + v.x, u.y + v.y, u.z + v.z);
}

inline Vector operator-(Vector u, Vector v)
{
    return Vector(u.x - v.x, u.y - v.y, u.z - v.z);
}

 

 

 

2.3 벡터 외적 (^ 연산자)

- 외적 연산자는 u와 v 사이의 외적을 취하고, u와 v에 모두 수직인 벡터를 반환한다.

- 두 벡터 u, v의 외적 u X v 는 u 벡터에서 v 벡터로의 회전을 의미한다.

 * 방향은 오른손 규칙(엄지 손가락 방향)에 따라 결정 된다.

 

- 3 개의 성분을 가진 두 벡터 u(x, y, z), v(x, y, z) 의 외적은 다음과 같다.

- 외적 연산은 분배법칙은 성립하나 교환법칙은 성립하지 않는다. (순서를 바꾸면 방향이 바뀐다.)

두 벡터의 외적

 

- 두 벡터가 평행을 이룰 경우 외적은 0 이 된다. 게임 내 충돌감지 시, 폴리곤 면에 수직인 법선벡터를 찾는 경우 등에 사용된다.

inline Vector operator^(Vector u, Vector v)
{
    return Vector(u.y * v.z - u.z * v.y,
        -u.x * v.z + u.z * v.x,
        u.x * v.y - u.y * v.x);
}

 

 

 

2.4 벡터 내적 (* 연산자)

- u와 v의 내적은 벡터 u를 v위에 투영한 것과 같다.

- 내적 P 는 다음과 같다.

두 벡터의 내적

- 벡터 위에 투영한 다른 벡터의 길이를 찾을 때 사용, 한 물체의 정점에서 다른 물체의 폴리곤 면 까지의 최단 거리 등을 찾는 경우 사용된다.

inline float operator*(Vector u, Vector v)
{
    return (u.x * v.x + u.y * v.y + u.z * v.z);
}

 

 

2.5 스칼라 곱

2.6 스칼라 나눗셈

- 앞선 곱, 나눗셈과 동일하다, 곱셈의 경우 float형의 위치에 따른 두 가지 경우에 대해 오버로딩 해준다.

inline Vector operator*(float s, Vector u)
{
    return Vector(u.x * s, u.y * s, u.z * s);
}
inline Vector operator*(Vector u, float s)
{
    return Vector(u.x * s, u.y * s, u.z * s);
}

 

 

 

2.7 스칼라 삼중곱 (TripleScalarProduct)

- 3 가지의 벡터u, v, w에 대한 스칼라 삼중곱을 구한다.

- 두개의 벡터 곱을 나머지 하나의 벡터와 곱한다.

 

- 기하학적 의미로 스칼라 삼중곱의 절대값은 평행육면체의 부피를 나타낸다.

기하학적 의미

 

- v와 w를 외적하고, 그 결과를 u와 내적한다. (u · (v X w))

inline float TripleScalarProduct(Vector u, Vector v, Vector w)
{
    return float((u.x * (v.y * w.z - v.z * w.y)) +
        (u.y * (-v.x * w.z + v.z * w.x)) +
        (u.z * (v.x * w.y - v.y * w.x)));
}