-
[Algorithm] MST, Minimun Spanning Tree알고리즘/Algorithm Theory 2024. 2. 21. 10:38
- MST : 그래프의 모든 정점을 연결하는 최소 비용 트리
1) Kruskal 크루스칼
- 간선들을 가중치를 기준으로 오름차순 정렬
- 사이클이 생기지 않는 간선을 (정점의 개수 - 1) 개 만큼 뽑아냄
2) Prim 프림
- 최소 힙을 사용하여, 각 정점으로 부터 최소 간선을 선택해나감
- 크루스칼 알고리즘


그래프 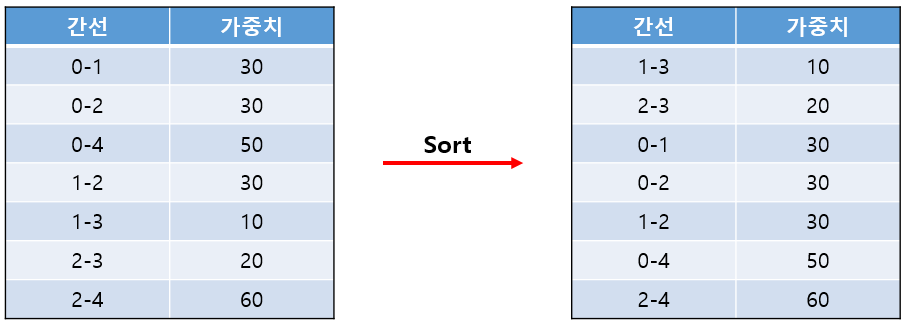
1. 정렬 
2. N - 1 개 간선 뽑기 - 크루스칼 구현
#include <iostream> #include <vector> #include <algorithm> using namespace std; int N = 5; struct Node { int a, b; int price; }; vector<Node> line; int arr[10]; bool compare(Node t, Node v) { return t.price < v.price; } void Init() { for (int i = 0; i < N; ++i) arr[i] = i; } int Find(int curr) { if (arr[curr] == curr) return curr; int ret = Find(arr[curr]); arr[curr] = ret; return ret; } void Union(int a, int b) { int r1 = Find(a); int r2 = Find(b); if (r1 == r2) return; arr[r2] = r1; } int main() { Init(); line = { {0, 1, 30}, {0, 2, 30}, {0, 4, 50}, {1, 2, 30}, {1, 3, 10}, {2, 3, 20}, {2, 4, 60} }; sort(line.begin(), line.end(), compare); int target = N - 1; // N - 1개를 뽑아내면 끝 int result = 0; //비용의 합 int selectCount = 0; for (Node node : line) { int a = node.a; int b = node.b; int price = node.price; if (Find(a) == Find(b)) continue; Union(a, b); result += price; selectCount++; if (selectCount == target) break; } cout << "결과 : " << result; return 0; }- 크루스칼 응용
1. 점 좌표 거리, 2차원 배열 점 : 각 목표위치간의 거리를 구하고 MST
2. 조건이 있는 MST : 사이클이 아니고, 조건~~를 만족하면 Union
3. MST + DFS : DFS 거리구하기 + MST
'알고리즘 > Algorithm Theory' 카테고리의 다른 글
세그먼트 트리 (Segment Tree) (2) 2024.03.12 [Algorithm] Binary Search, Two Pointer (0) 2024.02.26 [Algorithm] Union-Find (2) 2024.02.20 [Backtracking] Subset Sum (0) 2022.06.25 [D&C] Binary Search (0) 2022.06.25