[Linear model]리지 회귀

books.google.co.kr/books?id=tPaTDwAAQBAJ&lpg=PP1&dq=%ED%8C%8C%EC%9D%B4%EC%8D%AC%EB%9D%BC%EC%9D%B4%EB%B8%8C%EB%9F%AC%EB%A6%AC%EB%A5%BC%20%ED%99%9C%EC%9A%A9%ED%95%9C%20%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D&hl=ko&pg=PA1#v=onepage&q=%ED%8C%8C%EC%9D%B4%EC%8D%AC%EB%9D%BC%EC%9D%B4%EB%B8%8C%EB%9F%AC%EB%A6%AC%EB%A5%BC%20%ED%99%9C%EC%9A%A9%ED%95%9C%20%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D&f=false

파이썬 라이브러리를 활용한 머신러닝(번역개정판)

 

- 리지 회귀 모델

 

리지, Ridge는 회귀를 위한 선형 모델이다.

최소 제곱법과 마찬가지로, 회귀를 위한 선형 모델이므로 아래 예측 함수를 사용한다.

예측 함수

하지만 리지 회귀에서는 가중치(w)의 절댓값을 가능한 작게 만든다. w가 최대한 0에 가깝게)

즉, 특성들이 타겟값에 주는 영향이 최소화 되게 만든다.

 

 

 

- 규제(regularization)

 

가중치(w)의 절대값을 가능한 작게하여, 특성들이 결과에 주는 영향이 최소화 되게 한다.

위와 같은 제약을 규제라고 한다.

규제 : 과대적합이 되지 않도록 모델을 강제로 제한함

리지 회귀에는 L2 규제가 사용된다.

 

 

 

- L2 규제

 

손실함수, 평균제곱오차(MSE) 식에 아래 항이 추가된다.

* 손실함수 : 머신러닝이 학습할 수 있는 지표, 손실 함수 값이 최소화되도록 가중치와 편향을 찾는다. 평균제곱오차는 손실함수 중 하나이다.

 

MSE(손실함수)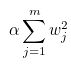

추가된 항

* α값을 크게하면 패널티의 효과가 커지고, α값을 작게하면 패널티의 효과가 작아진다.

---

 

- 리지 회귀

 

Ridge Model

Ridge모델은 모델의 복잡도를 제어할 alpha 매개변수가 존재한다.

alpha가 10일 때는 패널티 효과가 커져, 특성들이 주는 영향이 적어지고 상대적으로 과소적합이 된다. (모델 복잡도 감소)

alpha가 0.1일 때는 패널티 효과가 작아져, 그 반대가 된다.

 

alpha값을 높이면 모델의 복잡도 감소, alpha값을 낮추면 모델의 복잡도 증가

 

- code

#Ridge Regression
from sklearn.linear_model import Ridge
from mglearn.datasets import load_extended_boston
from sklearn.model_selection import train_test_split
X, y = load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
ridge = Ridge().fit(X_train, y_train) #alpha매개변수의 기본 값은 1.0
print('alpha가 기본 값, 1.0일 때')
print("training set score : %.2f" %(ridge.score(X_train, y_train)))
print("test set score : %.2f" %(ridge.score(X_test, y_test)))
ridge2 = Ridge(alpha=10).fit(X_train, y_train) #10
print('\nalpha가 10일 때')
print("training set score : %.2f" %(ridge2.score(X_train, y_train)))
print("test set score : %.2f" %(ridge2.score(X_test, y_test)))
ridge3 = Ridge(alpha=0.1).fit(X_train, y_train) #0.1
print('\nalpha가 0.1일 때')
print("training set score : %.2f" %(ridge3.score(X_train, y_train)))
print("test set score : %.2f" %(ridge3.score(X_test, y_test)))