[백준] 12752번 - 도시들
문제
https://www.acmicpc.net/problem/12752
풀이
특별한 알고리즘은 없고, 단순 다익스트라 문제이다.
많은 도시들이 있고 그 중 K(K <= 5)개의 도시를 연결하는 도로의 최소 비용을 구하면 된다.
1. K = 1
도로가 필요 없음
2. K = 2
두 개의 도시를 연결하는 최소 비용을 구하면 된다. 간단하게 다익스트라 1번으로 구할 수 있다.
3. K = 3
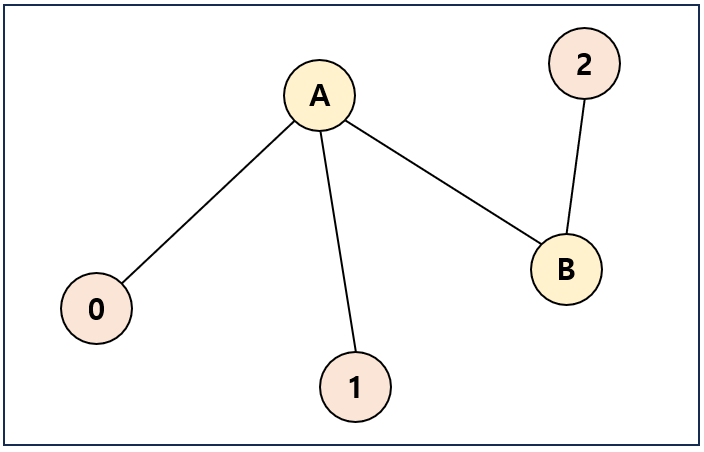
아래와 같은 경우들이 있을 수 있다. 각 점에서 출발해서 어떤 점에서 만난다고 생각하면 쉽다. K개의 도시(0, 1, 2 정점)
N개의 정점에서 만나는 경우 중 비용 합의 최소 값을 구한다.
A정점에서 만나는 경우: cost[0][A] + cost[1][A] + cost[2][A]
B정점에서 만나는 경우: cost[0][B] + cost[1][B] + cost[2][B]
...
4. K = 4
중복으로 더해지는 간선이 존재할 수 있다. 아래와 같은 경우는 K=3일 때와 같이 답을 구할 수 있지만,

이렇게 되버리면 중복으로 더해지는 간선이 생기게 된다.

따라서 두 점씩 묶어서 계산해주면 된다. 하지만 아래와 같은 경우가 생길 수 있기 때문에 모든 조합을 고려해서 최소 비용을 구해줘야 한다.
(0, 2), (1, 3)으로 조합할 경우 A또는 B에서 만날 때 AB 간선이 중복으로 합해진다.
(0, 1), (2, 3)으로 조합하면 A정점에서 만날 때 cost[0][1][A] + cost[2][3][A]로 답을 구할 수 있다.


5. K = 5
두 개의 그룹으로 묶을 수 없기 때문에 3개의 그룹(2, 2, 1)으로 묶어주고 마찬가지로 모두 계산하면서 답을 구해주면 된다.
코드
풀 때는 몰랐는데 지금 보니까 N < 100,000 이었음
조합을 따로 구하려다가 몇 개 없길래 그냥 품
#include <vector>
#include <cstring>
#include <queue>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int N, K, M;
struct Node {
int n;
long long cost;
bool operator<(const Node& o) const {
return cost > o.cost;
}
};
priority_queue<Node> pq;
long long ret[5][200001];
long long result[5][5][200001];
vector<Node> graph[200001];
int hashMap[5];
void dijkstra(int index) {
int start = hashMap[index];
for (int i = 1; i <= N; ++i) {
//10^15
ret[index][i] = 1000000000000000;
}
pq.push({ start, 0 });
ret[index][start] = 0;
while (!pq.empty()) {
Node now = pq.top();
pq.pop();
if (now.cost > ret[index][now.n]) continue;
for (int i = 0; i < graph[now.n].size(); ++i) {
Node nxt = graph[now.n][i];
long long nxtCost = nxt.cost + ret[index][now.n];
if (nxtCost >= ret[index][nxt.n]) continue;
ret[index][nxt.n] = nxtCost;
pq.push({ nxt.n, nxtCost });
}
}
}
void dijkstra2(int a, int b) {
for (int i = 1; i <= N; ++i) {
//a, b, i
result[a][b][i] = ret[a][i] + ret[b][i];
pq.push({ i, result[a][b][i] });
}
//a, b로부터 어떤x의 최단거리
while (!pq.empty())
{
Node now = pq.top();
pq.pop();
if (now.cost > result[a][b][now.n]) continue;
for (int i = 0; i < graph[now.n].size(); ++i) {
Node nxt = graph[now.n][i];
long long nxtCost = nxt.cost + result[a][b][now.n];
if (result[a][b][nxt.n] <= nxtCost) continue;
result[a][b][nxt.n] = nxtCost;
pq.push({ nxt.n, nxtCost });
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> K >> M;
for (int i = 0; i < K; ++i) {
cin >> hashMap[i];
}
for (int i = 0; i < M; ++i) {
int a, b;
long long c;
cin >> a >> b >> c;
graph[a].push_back({ b, c });
graph[b].push_back({ a, c });
}
// 다익
for (int i = 0; i < K; ++i) {
dijkstra(i);
}
// K 3이하는 중복이 일어나진 않음
if (K < 4) {
int minIndex = 0;
long long minCost = 5000000000000000;
for (int i = 1; i <= N; ++i) {
long long currCost = 0;
for (int j = 0; j < K; ++j) {
currCost += ret[j][i];
}
if (minCost > currCost) {
minCost = currCost;
minIndex = i;
}
}
cout << minCost;
}
else if (K == 4) {
for (int a = 0; a < K - 1; ++a) {
for (int b = a + 1; b < K; ++b) {
//10개 case. -> 다익 10개?
dijkstra2(a, b);
}
}
int gp[3][4] = {
{0, 1, 2, 3}
,{0, 2, 1, 3}
,{0, 3, 1, 2}
};
int minIndex = 0;
long long minCost = 5000000000000000;
for (int i = 1; i <= N; ++i) {
for (int g = 0; g < 3; ++g) {
long long currCost = result[gp[g][0]][gp[g][1]][i] + result[gp[g][2]][gp[g][3]][i];
if (minCost > currCost) {
minCost = currCost;
minIndex = i;
}
}
}
cout << minCost;
}
else if (K == 5) {
//5 * 3개 = 15
for (int a = 0; a < K - 1; ++a) {
for (int b = a + 1; b < K; ++b) {
//10개 case. -> 다익 10개?
dijkstra2(a, b);
}
}
int gp[15][5] = {
{0, 1, 2, 3, 4},{0, 2, 1, 3, 4},{0, 3, 1, 2, 4},
{0, 1, 2, 4, 3},{0, 2, 1, 4, 3},{0, 4, 1, 2, 3},
{0, 1, 3, 4, 2},{0, 4, 1, 3, 2},{0, 3, 1, 4, 2},
{0, 4, 2, 3, 1},{0, 2, 3, 4, 1},{0, 3, 2, 4, 1},
{1, 4, 2, 3, 0},{2, 4, 1, 3, 0},{3, 4, 1, 2, 0},
};
int minIndex = 0;
long long minCost = 5000000000000000;
for (int i = 1; i <= N; ++i) {
for (int g = 0; g < 15; ++g) {
long long currCost = result[gp[g][0]][gp[g][1]][i] + result[gp[g][2]][gp[g][3]][i] + ret[gp[g][4]][i];
if (minCost > currCost) {
minCost = currCost;
minIndex = i;
}
}
}
cout << minCost;
}
return 0;
}